Arithmatical – Alligation or Mixture
DIRECTIONS : Important Facts and Formulae
| 1. |
A container contains 40 litres of milk. From this container 4 litres of milk was taken out and replaced by water. This process was repeated further two times. How much milk is now contained by the container. |
| |
A. 26.34 litres |
| |
B. 27.36 liters |
| |
C. 28 litres |
| |
D. 29.16 litres |
| Solution |
| Amount of milk left after 3 operations |
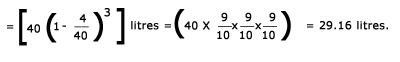 |
|
| 2. |
Tea worth Rs.126 per kg are mixed with a third variety in the ratio 1: 1 : 2. If the mixture is worth Rs.153 per kg, the price of the third variety per kg will be |
| |
A. Rs.169.50 |
| |
B. Rs.1700 |
| |
C. Rs. 175.50 |
| |
D. Rs. 180 |
| Solution |
| |
|
Since first second varieties are mixed in equal proportions, so their average price = Rs.(126+135/2) = Rs.130.50 |
| So, the mixture is formed by mixing two varieties, one at Rs. 130.50 per kg and the other at say, Rs. x per kg in the ratio 2 : 2, i.e., 1 : 1. We have to find x. |
| Cost of 1 kg tea of 1st kind |
Cost of 1 kg tea of 2nd kind |
 |
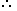 x-153/22.50 = 1 =› x - 153 = 22.50 =› x=175.50. x-153/22.50 = 1 =› x - 153 = 22.50 =› x=175.50. |
| Hence, price of the third variety = Rs.175.50 per kg. |
|
| 3. |
A milk vendor has 2 cans of milk. The first contains 25% water and the rest milk. The second contains 50% water. How much milk should he mix from each of the containers so as to get 12 litres of milk such that the ratio of water to milk is 3 : 5? |
| |
A. 4 litres, 8 litres |
| |
B. 6 litres, 6 litres |
| |
C. 5 litres, 7 litres |
| |
D. 7 litres, 4 litres |
| Solution |
| |
|
Let the cost of 1 litre milk be Re. 1 |
| Milk in 1 litre mix. in 1st can = 3/4 litre, C.P. of 1 litre mix. in 1st can Re. 3/4 |
| Milk in 1 litre mix. in 2nd can = 1/2 litre, C.P. of 1 litre mix. in 2nd can Re. 1/2 |
| Milk in 1 litre of final mix. = 5/8 litre, mean price = Re. 5/8. |
| By the rule of alligation, we have: |
| Cost of 1 kg mixture of 1st kind |
Cost of 1 kg mixture of 2nd kind |
 |
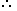 Ratio of two mixtures = 1/8 : 1/8 = 1:1. Ratio of two mixtures = 1/8 : 1/8 = 1:1. |
| So, quantity of mixture taken from each can = (1/2 X 12) = 6 litres. |
|
| 4. |
Two vessels A and B contain spirit and water in the ratio 5 : 2 and 7 : 6 respectively. Find the ratio in which these mixture be mixed to obtain a new mixture in vessel C containing spirit and water in the ration 8 : 5? |
| |
A. 4 : 3 |
| |
B. 3 : 4 |
| |
C. 5 : 6 |
| |
D. 7 : 9 |
| Solution |
| |
|
Let the C.P. of spirit be Re. 1 litre. |
| Spirit in 1 litre mix. of A = 5/7 litre, C.P. of 1 litre mix. in A = Re. 5/7 |
| Spirit in 1 litre mix. of B = 7/13 litre, C.P. of 1 litre mix. in B = Re. 7/13 |
| Spirit in 1 litre mix. of C = 8/13 litre, Mean price = Re. 8/13. |
| By the rule of alligation, we have: |
| Cost of 1 litre mixture in A |
Cost of 1 litre mixture in B |
 |
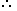 Required ratio = 1/13 : 9/91 = 7 : 9. Required ratio = 1/13 : 9/91 = 7 : 9. |
|
| 5. |
A can contains a mixture of two liquids A and B in the ratio 7 : 5. When 9 litres of mixture are drawn off and the can is filled with B, the ratio of A and B becomes
7 : 9. How many litres of liquid A was contained by the can initially? |
| |
A. 10 |
| |
B. 20 |
| |
C. 21 |
| |
D. 25 |
| Solution |
| Suppose the can initially contains 7x and 5x litres of mixtures A and B respectively |
Quantity of A in mixture left
= (7x - 7/12 x 9) litres = (7x - 21/4) litres. |
Quantity of B in mixture left
= (5x - 5/12 x 9) litres = (5x - 15/4) litres. |
| (7x - 21/4) / [(5x - 15/4)+9] = 7/9 = › 28x - 21/20x + 21 = 7/9 =› 252x - 189 = 140x + 147 |
| |
=› 112x = 336 =’ x = 3. |
| So, the can contained 21 litres of A. |
|
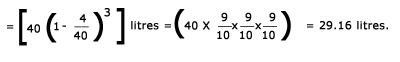

 x-153/22.50 = 1 =› x - 153 = 22.50 =› x=175.50.
x-153/22.50 = 1 =› x - 153 = 22.50 =› x=175.50.
